Найдите сумму всех трехзначных натуральных чисел, которые при делении на 19 дают в остатке 6.
Решение. Очевидно, что числа, которые при делении на 19 дают в остатке 6, образуют арифметическую прогрессию, задаваемую по формуле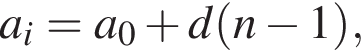 
где d = 19, а a0 — первый неотрицательный член прогрессии, то есть, число 6. Найдём первый и последний трёхзначные члены прогрессии:
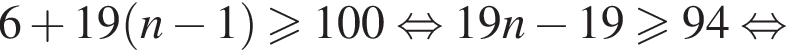
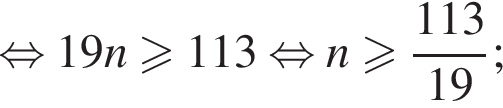
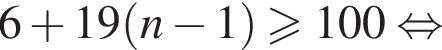
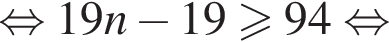
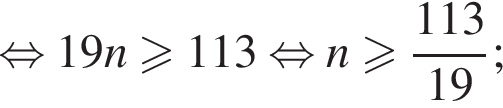
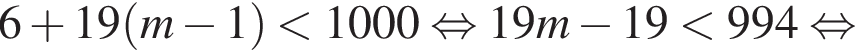
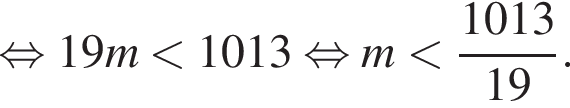
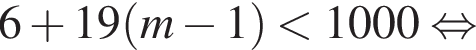
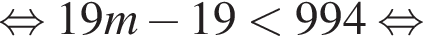
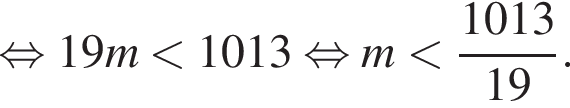
Так как n и m — целые числа, они равны соответственно 6 и 53, тогда первый и последний подходящие члены прогрессии равны 101 и 994, а количество искомых чисел равно 53 − 6 + 1 = 48. Сумма арифметической прогрессии равна полусумме первого и последнего члена, умноженной на количество чисел. В нашем случае:
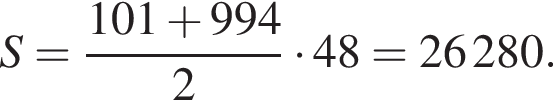
Ответ: 26 280.