РЕШУ ЦТ — математика–9

Задания

Задание № 35 Добавить в вариант

Классификатор алгебры: 3.2 Квадратные неравенства

Задания на 5 баллов

Решите квадратное неравенство 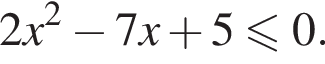$2x в квадрате минус 7x плюс 5 меньше или равно 0.$

Решение. Решим соответствующее квадратное уравнение, чтобы найти значения переменной, при которых неравенство обращается в верное равенство. Заметим, что сумма коэффициентов равна 0, а значит, один из корней равен 1. По теореме, обратной теореме Виета, второй корень равен отношению c к a, то есть, $дробь: числитель: 5, знаменатель: 2 конец дроби .$

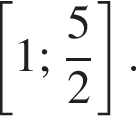
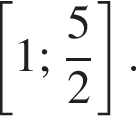
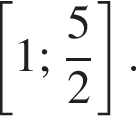
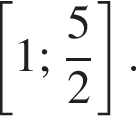
Уравнение задаёт на плоскости параболу, ветви которой направлены вверх, так как коэффициент при старшем члене положительный. Неравенство же задаёт на плоскости область, отсечённую ветвями параболы, так как знак  — меньше или равно. Иными словами, ответом является отрезок $левая квадратная скобка 1 ; дробь: числитель: 5, знаменатель: 2 конец дроби правая квадратная скобка .$

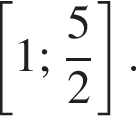
Ответ: $левая квадратная скобка 1 ; дробь: числитель: 5, знаменатель: 2 конец дроби правая квадратная скобка .$

$левая квадратная скобка 1 ; дробь: числитель: 5, знаменатель: 2 конец дроби правая квадратная скобка .$

Классификатор алгебры: 3.2 Квадратные неравенства

Источник: Вариант № 2

Ключ

№ п/п	№ задания	Ответ
1	35	$левая квадратная скобка 1 ; дробь: числитель: 5, знаменатель: 2 конец дроби правая квадратная скобка .$