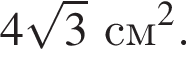Выберите два последовательных целых числа, между которыми заключено число ![]() :
:
а) 6 и 7
б) 9 и 10
в) 7 и 8
г) 8 и 9
Выберите два последовательных целых числа, между которыми заключено число ![]() :
:
а) 6 и 7
б) 9 и 10
в) 7 и 8
г) 8 и 9
Выберите верное равенство:
а) 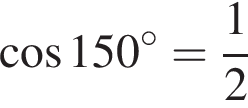
б) 
в) 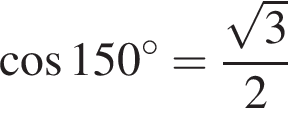
г) 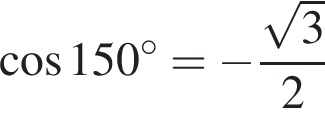
Один из смежных углов на 20° больше другого. Найдите эти углы.
На рисунке угол BOC = 142°, угол MOC = 90° и OK — биссектриса угла BOC. Найдите величину угла KOM.
Вычислите: 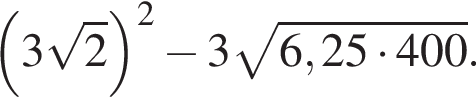
Вычислите: 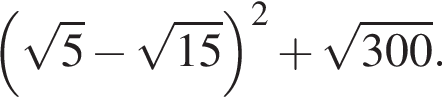
Решите неравенство 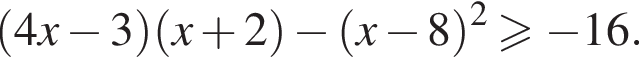
Найдите радиус окружности, описанной около треугольника со сторонами 13 см, 10 см и 13 см.
Диагональ ромба делит его высоту, проведенную из вершины тупого угла, на отрезки длиной 25 см и 15 см. Найдите периметр ромба.
Площадь вписанного в правильный многоугольник круга в 4 раза меньше площади круга, описанного около этого многоугольника. Найдите периметр многоугольника, если его площадь равна