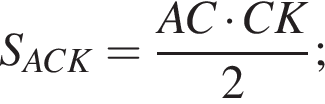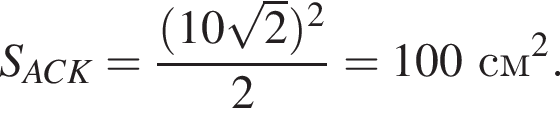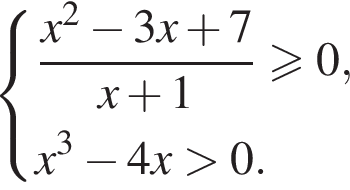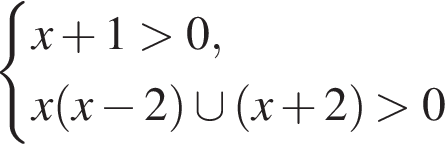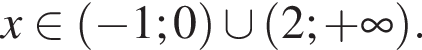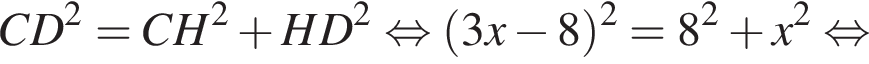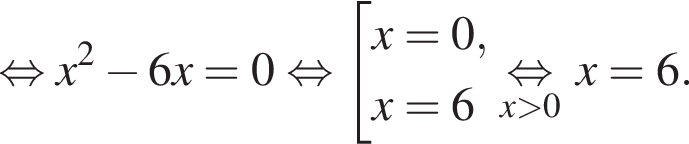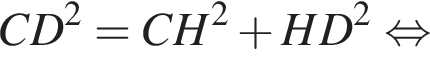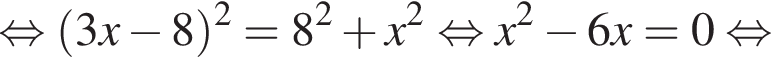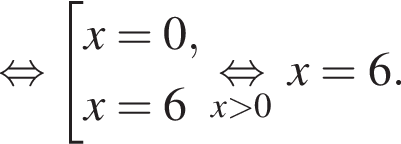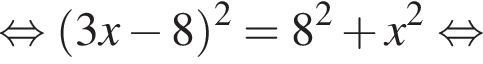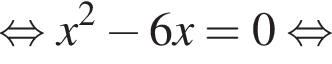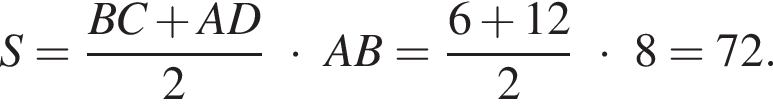1. Задание № 340 

Классификатор алгебры: 1.4 Действия с корнями из чисел
Источник: Вариант № 32
Задания на 10 баллов
i
Сравните значения выражений 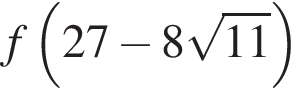 и
и  если
если  а
а 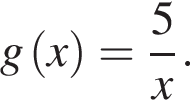
Решение. Найдём сначала значение 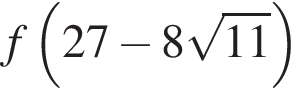 :
:
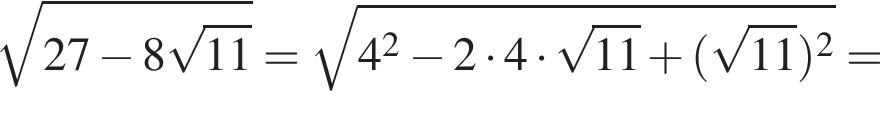
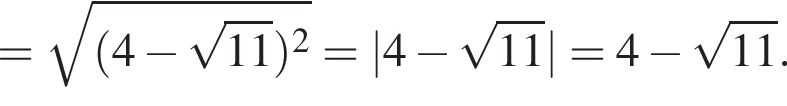
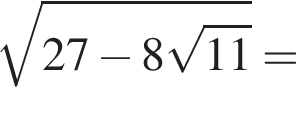
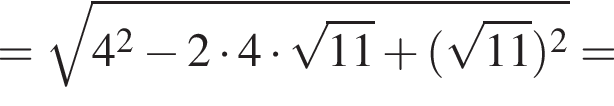
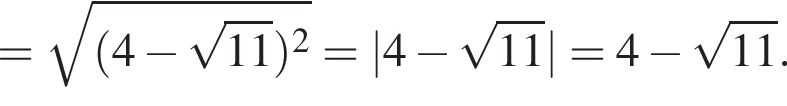
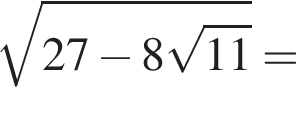
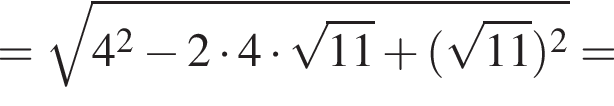
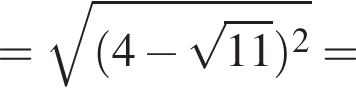
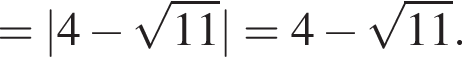
Теперь найдём значение 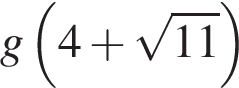 :
:
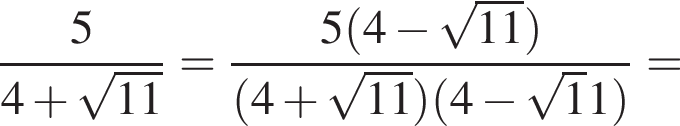
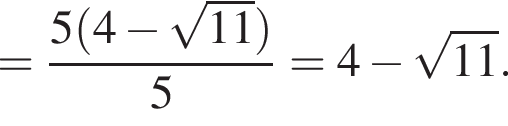
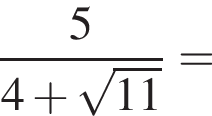
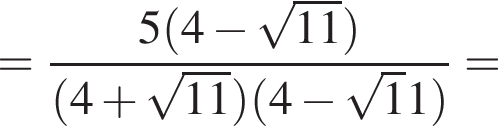
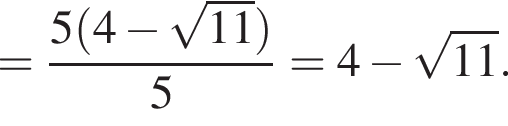
Получилось, что значения двух выражений равны.
Ответ: они равны.
Ответ: они равны.
340
они равны.
Классификатор алгебры: 1.4 Действия с корнями из чисел
Источник: Вариант № 32
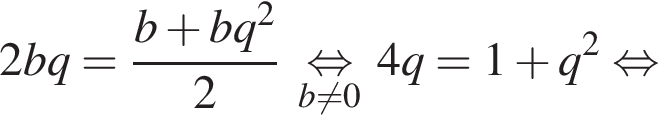
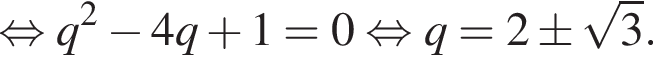
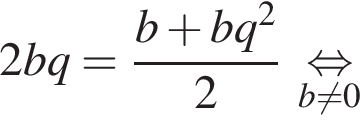
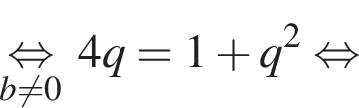
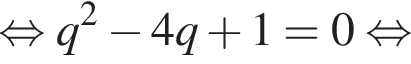
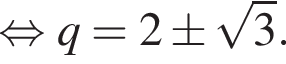
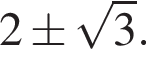
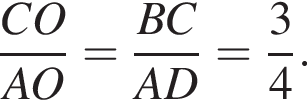
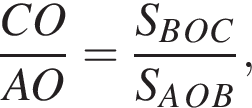 откуда
откуда 
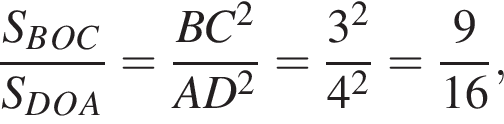 откуда
откуда 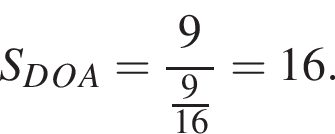
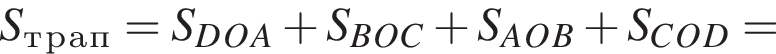
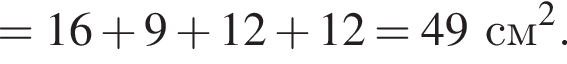



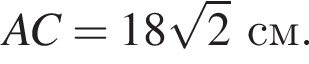 Радиус окружности, описанной около треугольника AMB, равен
Радиус окружности, описанной около треугольника AMB, равен 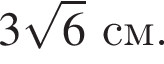 Найдите радиус окружности, описанной около треугольника BMC.
Найдите радиус окружности, описанной около треугольника BMC.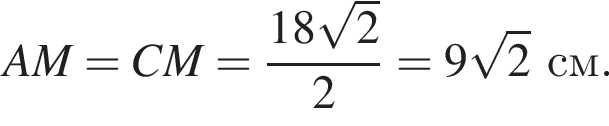
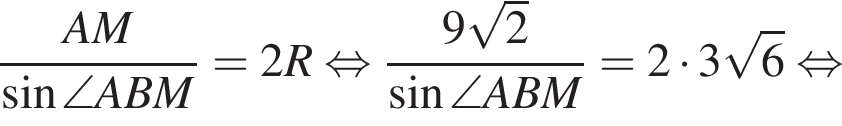
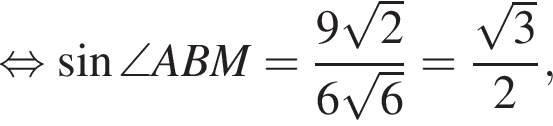
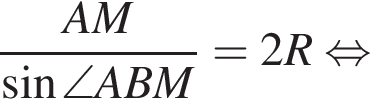
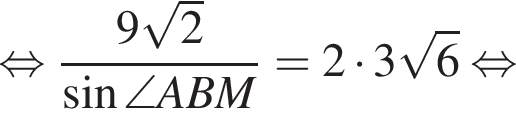
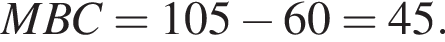 Снова воспользуемся теоремой синусов, но в треугольнике BMC:
Снова воспользуемся теоремой синусов, но в треугольнике BMC: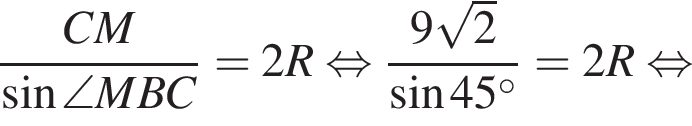
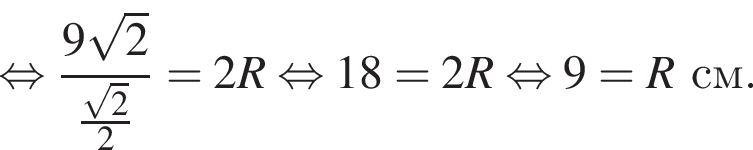
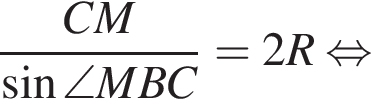
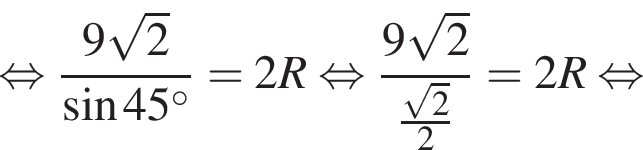

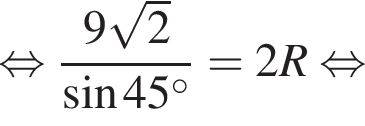
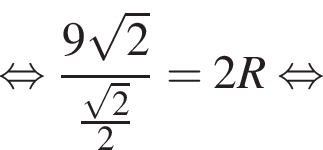
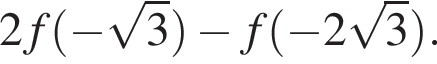
 Тогда
Тогда 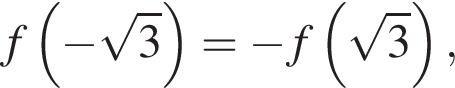 a
a 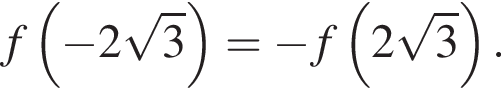 Найдем
Найдем  и
и 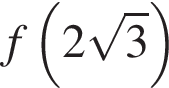 :
: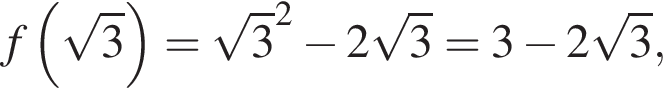
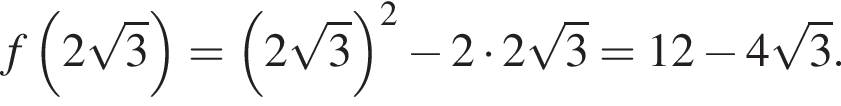
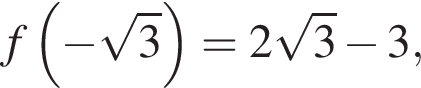
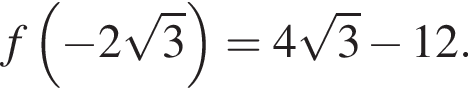 Подставим теперь известные значения в данное выражение:
Подставим теперь известные значения в данное выражение: 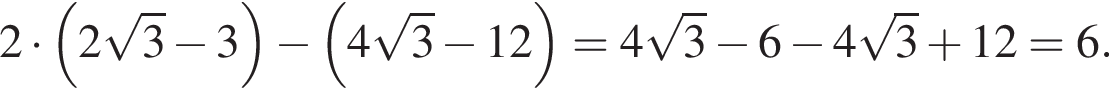
 то AD = 17 − AB.
то AD = 17 − AB.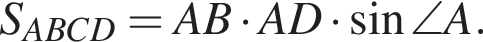
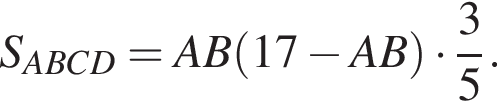
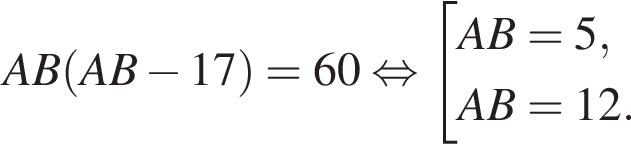
 Используя формулы приведения, получим:
Используя формулы приведения, получим:

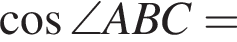

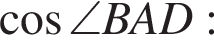
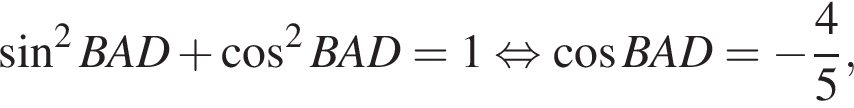
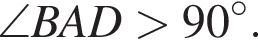
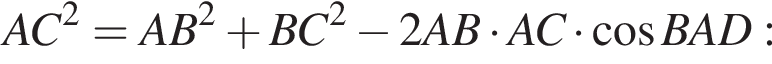
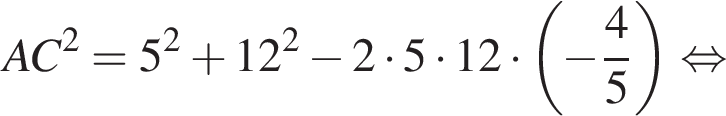

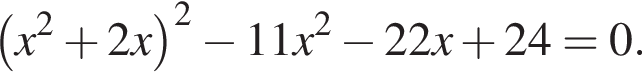
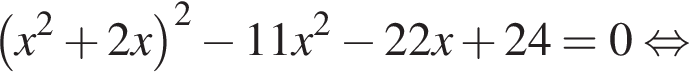
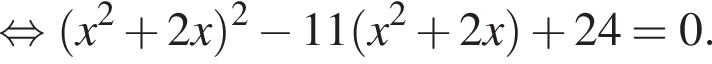
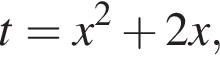 тогда решим вспомогательное уравнение
тогда решим вспомогательное уравнение 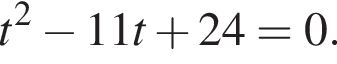 Используя обратную теорему Виета, имеем:
Используя обратную теорему Виета, имеем: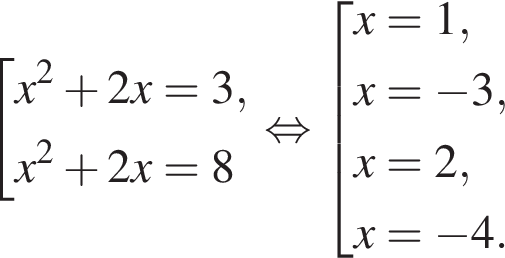
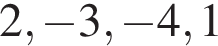 }.
}.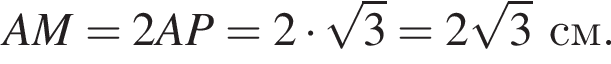
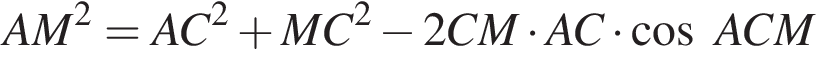
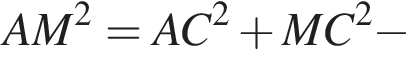

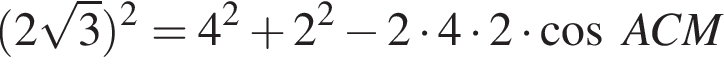
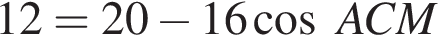
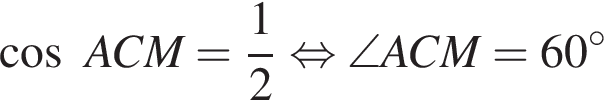

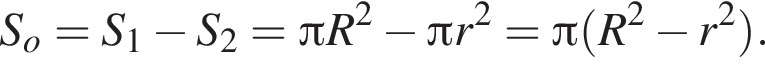 Так как
Так как  то
то 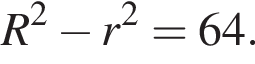 В прямоугольном треугольнике AOH найдём AH по теореме Пифагора:
В прямоугольном треугольнике AOH найдём AH по теореме Пифагора:  А значит, AH = 8, а AB = 16.
А значит, AH = 8, а AB = 16.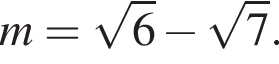 Докажите, что значение выражения
Докажите, что значение выражения 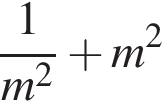 является целым числом.
является целым числом.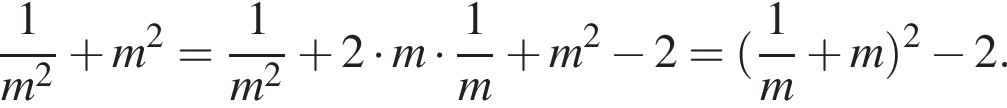
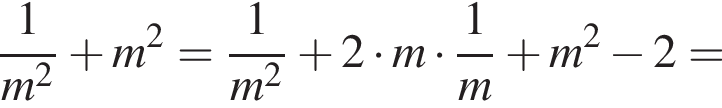
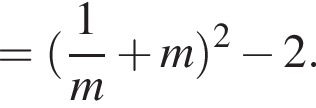
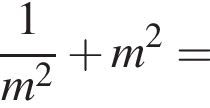
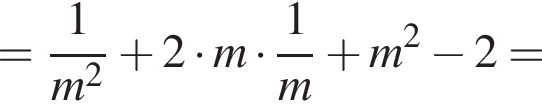
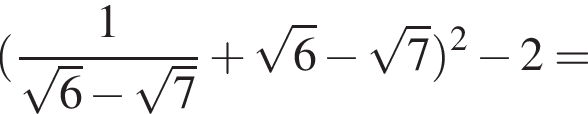
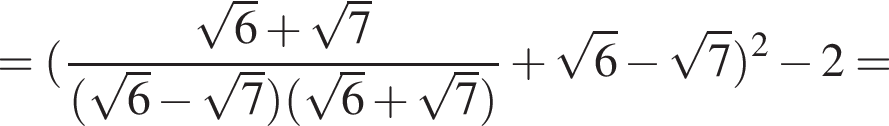
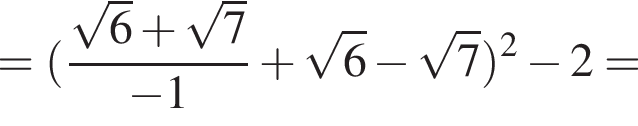

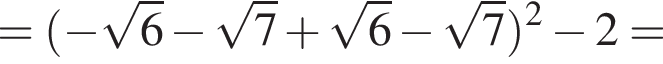

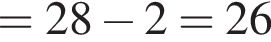 − целое число. Что и требовалось доказать.
− целое число. Что и требовалось доказать.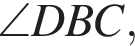 потому что они являются вписанными углами, которые опираются на равные части дуги. Следовательно, BD — биссектриса
потому что они являются вписанными углами, которые опираются на равные части дуги. Следовательно, BD — биссектриса 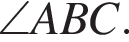 Тогда, по свойству биссектрисы, в треугольнике ABC выполнено отношение
Тогда, по свойству биссектрисы, в треугольнике ABC выполнено отношение  =
= 
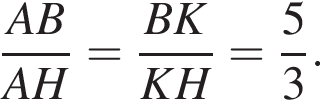
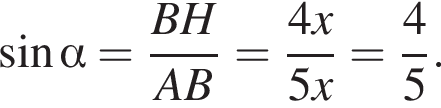
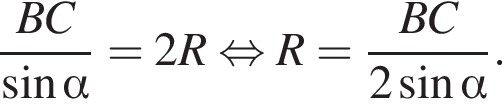 Подставим:
Подставим: 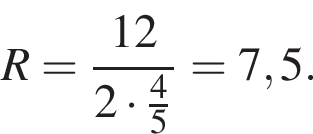
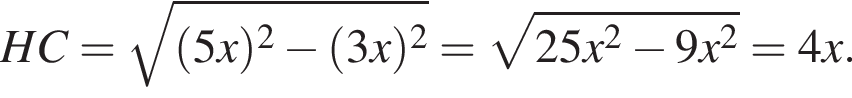
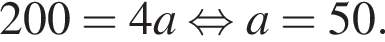
 тогда имеем:
тогда имеем: 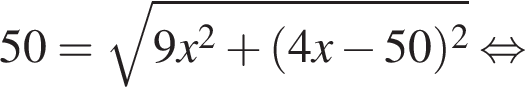
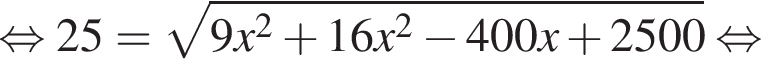
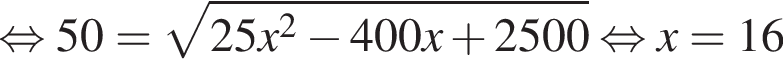

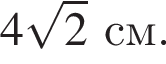 Найдите большую сторону этого треугольника.
Найдите большую сторону этого треугольника.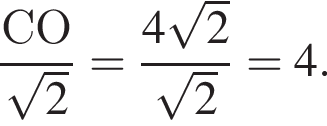 Центр вписанной окружности — точка пересечения биссектрис, поэтому
Центр вписанной окружности — точка пересечения биссектрис, поэтому 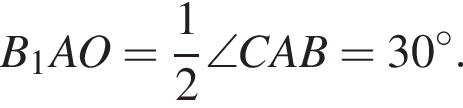

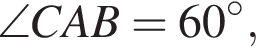
 Отрезок СА лежит против угла в 30° в прямоугольном треугольнике, значит, это половина гипотенузы, а гипотенуза является большей стороной прямоугольного треугольника:
Отрезок СА лежит против угла в 30° в прямоугольном треугольнике, значит, это половина гипотенузы, а гипотенуза является большей стороной прямоугольного треугольника: 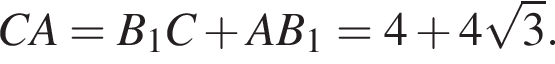

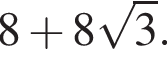
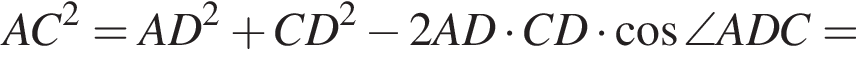
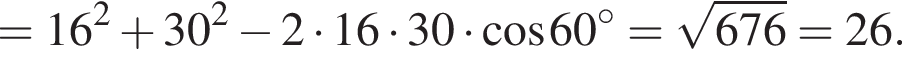
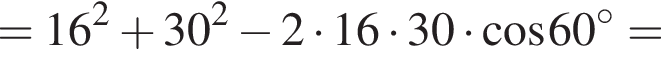

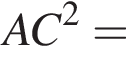

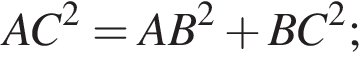
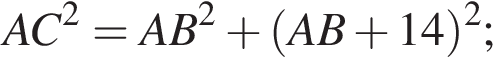
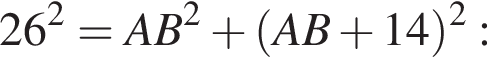
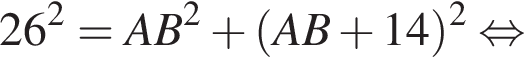
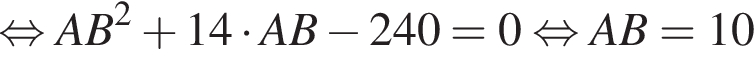
 (свойство ромба). Тогда
(свойство ромба). Тогда 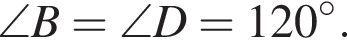 Так как дан ромб, BC = DC = 8, следовательно,
Так как дан ромб, BC = DC = 8, следовательно, 
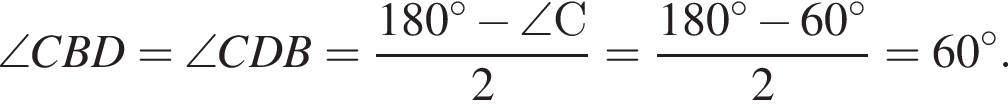
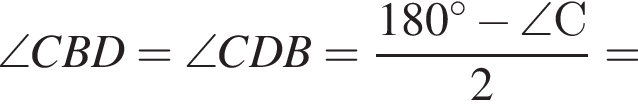
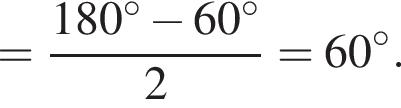

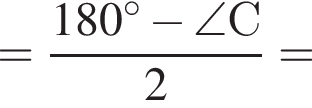
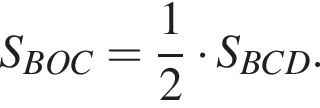
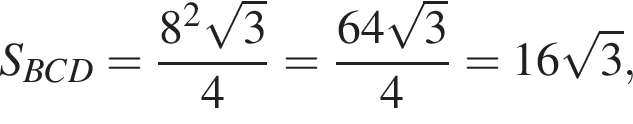
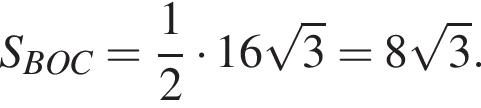
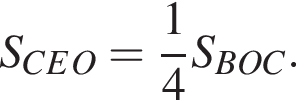 Имеем:
Имеем: 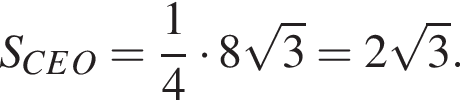

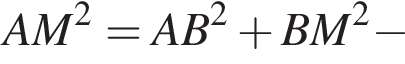
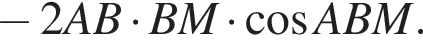
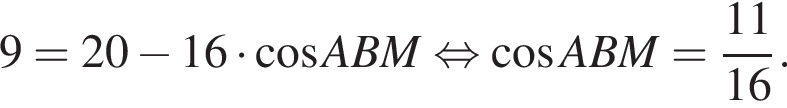
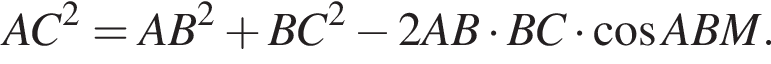
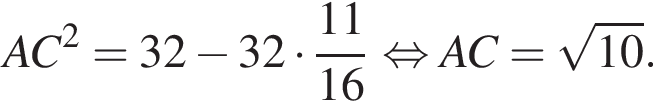
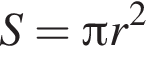 :
: 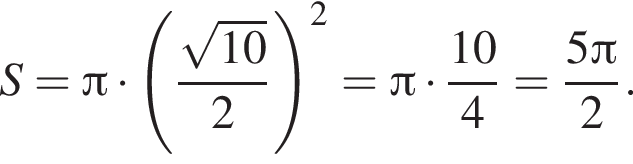
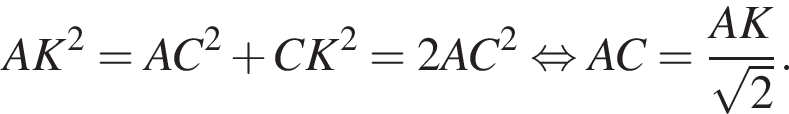
 Найдём площадь треугольника ACK:
Найдём площадь треугольника ACK: 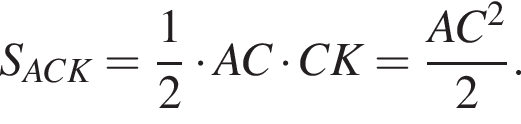
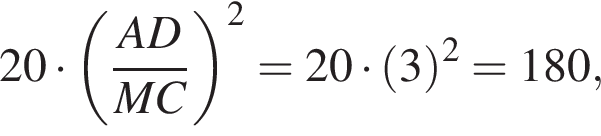 а площадь треугольника MAB равна
а площадь треугольника MAB равна 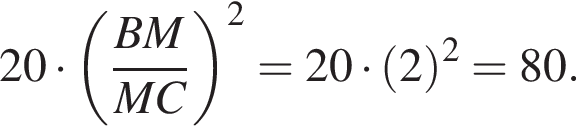 В таком случае площадь параллелограмма равна
В таком случае площадь параллелограмма равна 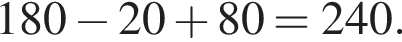
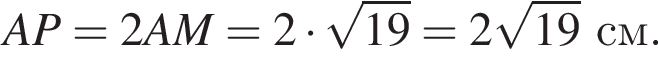

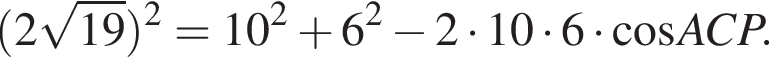
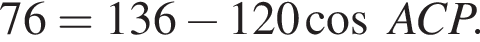
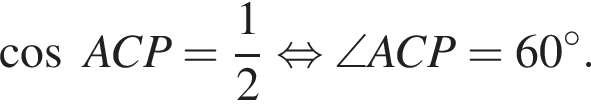
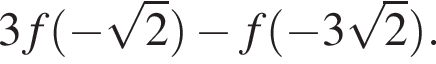
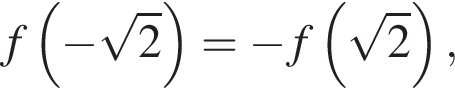 a
a 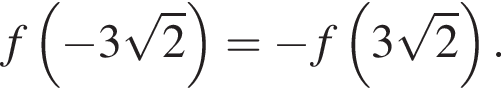 Найдем
Найдем  и
и 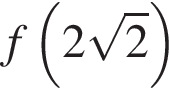 :
: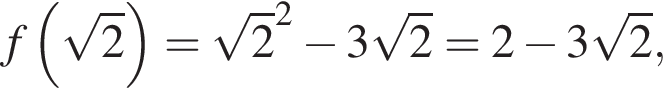
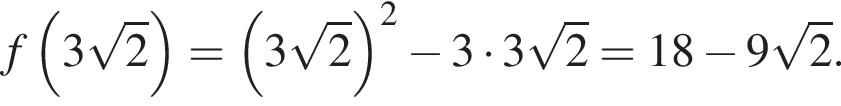
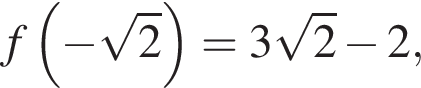
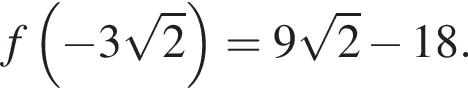 Подставим теперь известные значения в данное выражение:
Подставим теперь известные значения в данное выражение: 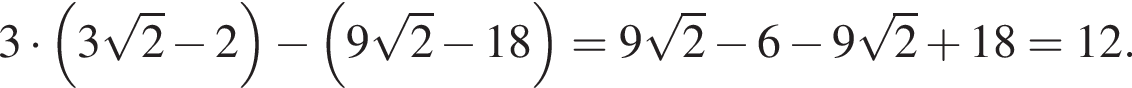
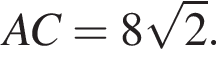 Найдём площадь треугольника ACK:
Найдём площадь треугольника ACK: 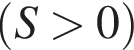 —
—

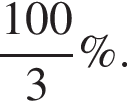
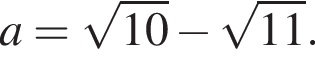 Докажите, что значение выражения
Докажите, что значение выражения 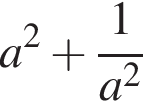 является целым числом.
является целым числом.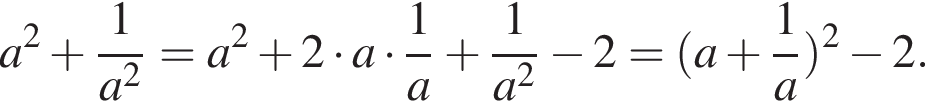
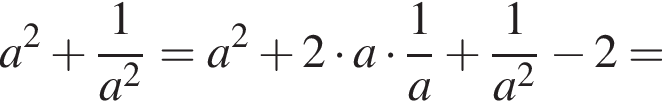
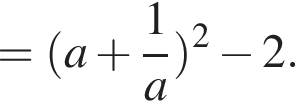
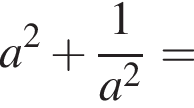
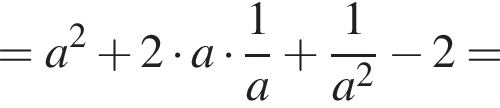
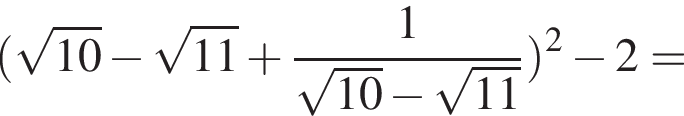
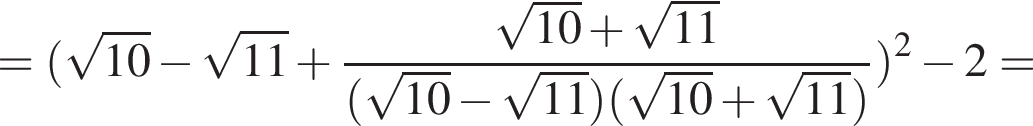
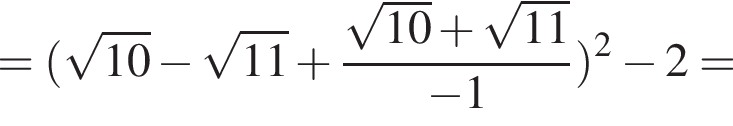
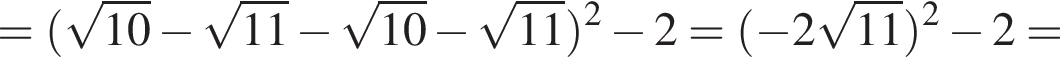
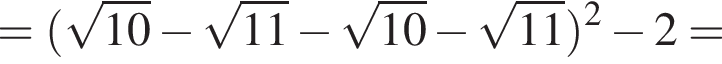
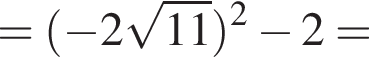
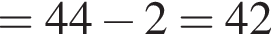 — целое число. Что и требовалось доказать.
— целое число. Что и требовалось доказать.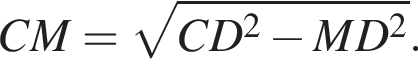
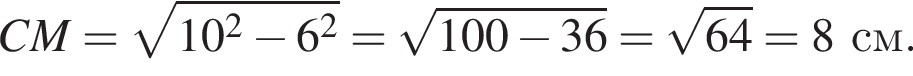
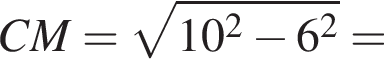
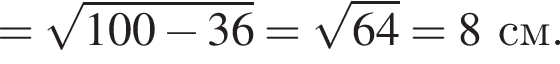
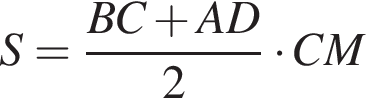 :
: 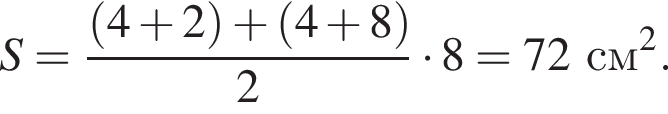
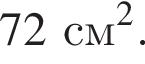
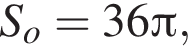 то
то 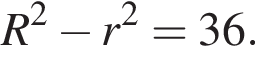 В прямоугольном треугольнике AOH найдём AH по теореме Пифагора:
В прямоугольном треугольнике AOH найдём AH по теореме Пифагора:  А значит, AH = 6, а AB = 12.
А значит, AH = 6, а AB = 12.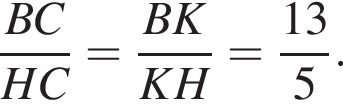
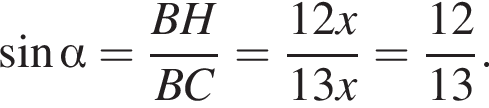
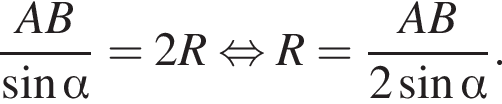 Подставим:
Подставим: 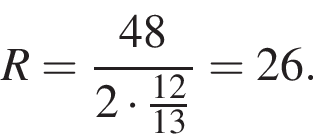
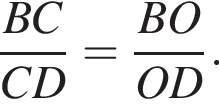 Так как BO : OD = 3 : 13, то BC : CD = 3 : 13.
Так как BO : OD = 3 : 13, то BC : CD = 3 : 13.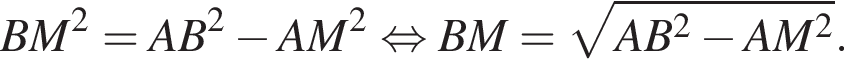
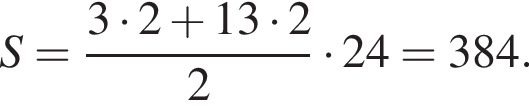
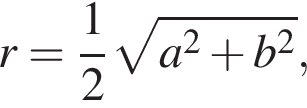 где a,b - катеты треугольника:
где a,b - катеты треугольника: 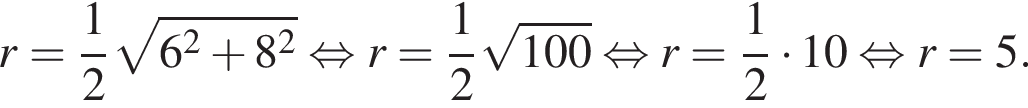

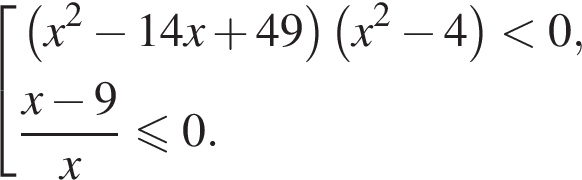

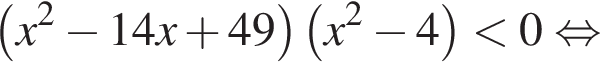
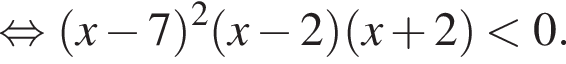
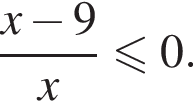 Найдём объединение множеств решений (см.рис.).
Найдём объединение множеств решений (см.рис.).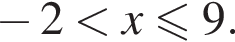
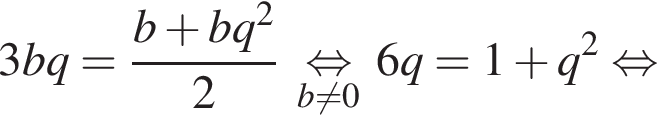
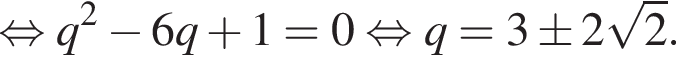
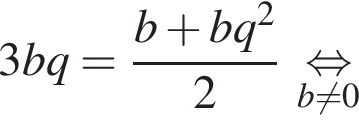
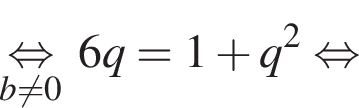
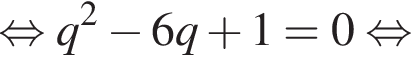
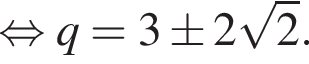

 тогда радиус больше окружности равен 6. Заметим, что треугольники AO1M и AO2K подобны по двум равным углам, один из которых прямой, а второй — общий. Тогда из подобия треугольников получаем равенство отношений их сторон
тогда радиус больше окружности равен 6. Заметим, что треугольники AO1M и AO2K подобны по двум равным углам, один из которых прямой, а второй — общий. Тогда из подобия треугольников получаем равенство отношений их сторон 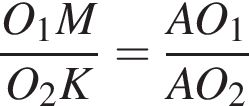 :
: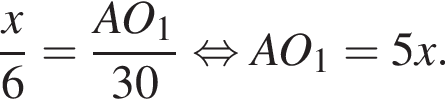
 Последним шагом нашего решения найдём длину окружности по формуле, приведённой выше
Последним шагом нашего решения найдём длину окружности по формуле, приведённой выше 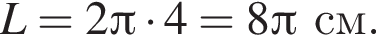
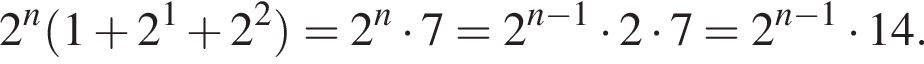
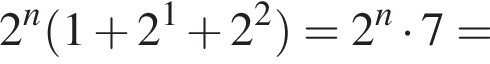
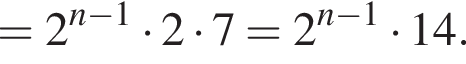

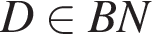 Найдите радиус окружности, если
Найдите радиус окружности, если 

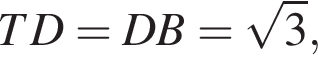 а
а 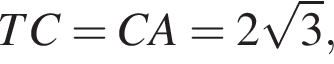 тогда
тогда 
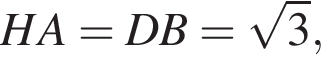 и
и 
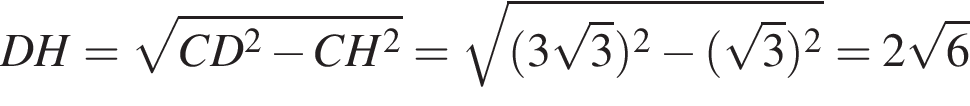
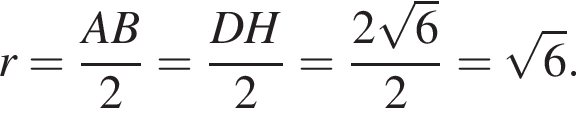
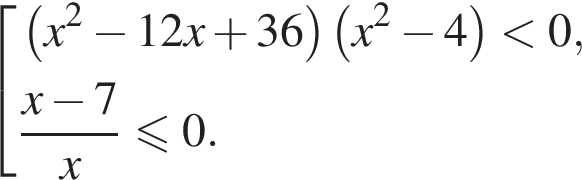

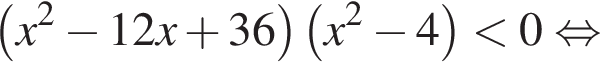
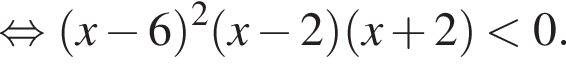
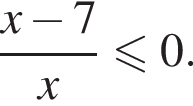 Найдём объединение множеств решений (см.рис.).
Найдём объединение множеств решений (см.рис.). 
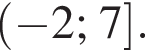
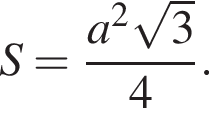 Имеем
Имеем 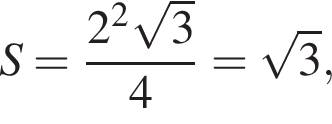 а площадь трапеции в таком случае равна
а площадь трапеции в таком случае равна 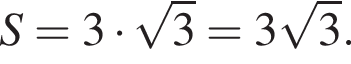


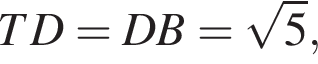 а
а 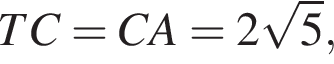 тогда
тогда 
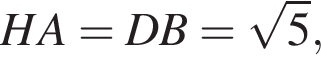 и
и 
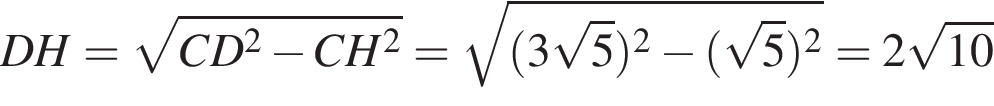
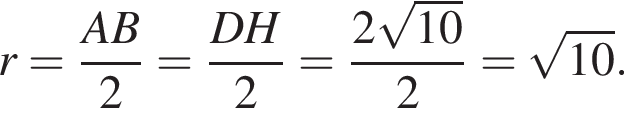
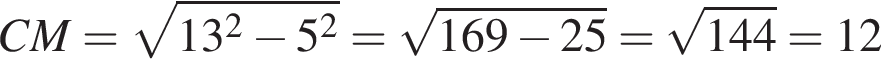
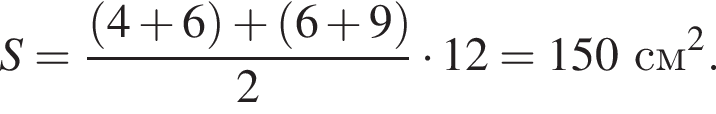
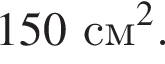
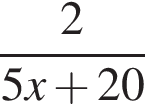
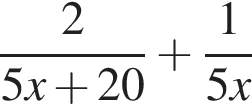
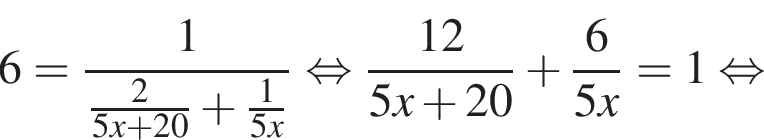
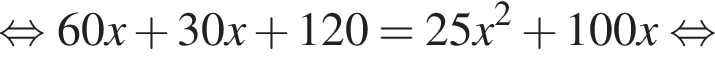
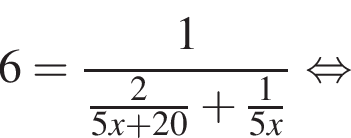
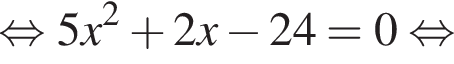
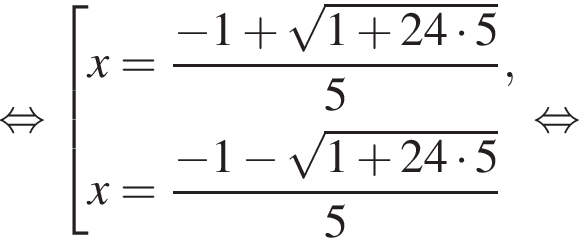
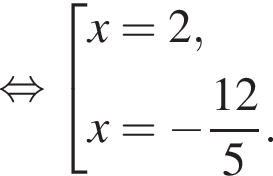
 часов.
часов.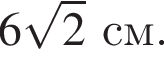 Найдите большую сторону этого треугольника.
Найдите большую сторону этого треугольника.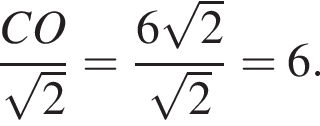 Центр вписанной окружности — точка пересечения биссектрис, поэтому
Центр вписанной окружности — точка пересечения биссектрис, поэтому 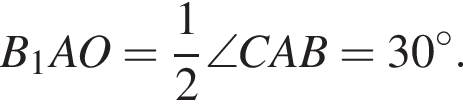

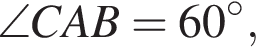
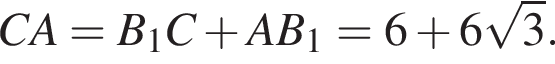
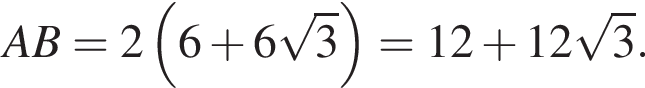
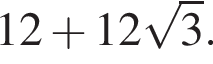
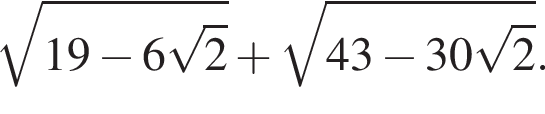
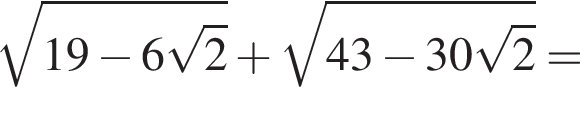
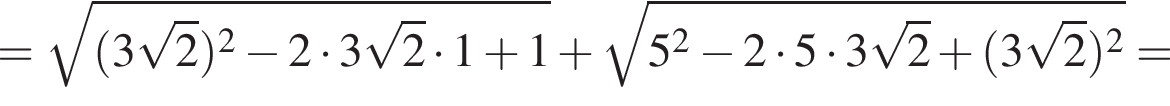
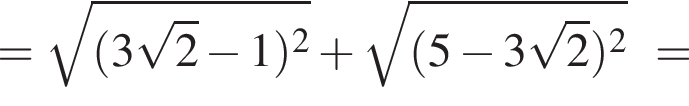


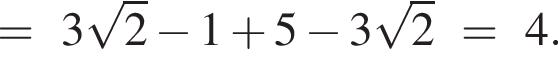
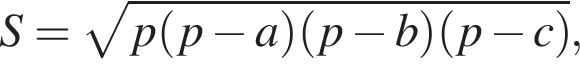 где p — полупериметр, а a, b, c — стороны треугольника. В нашем случае полупериметр равен
где p — полупериметр, а a, b, c — стороны треугольника. В нашем случае полупериметр равен 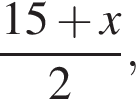 имеем
имеем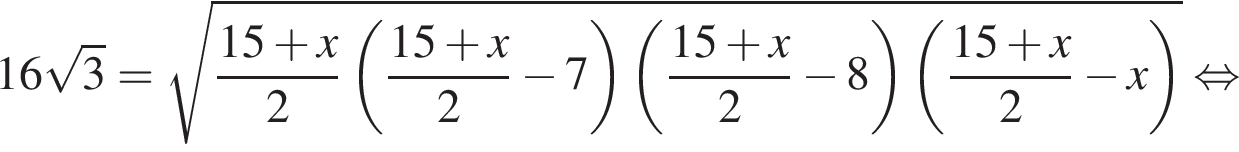
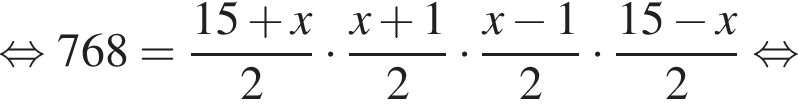
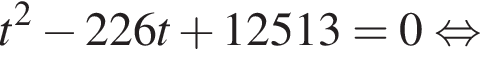
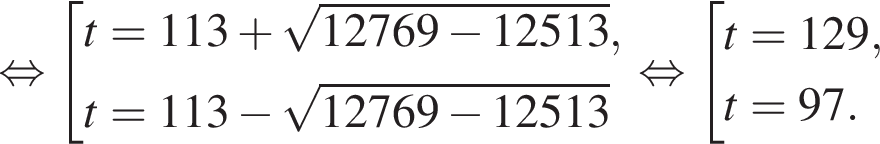
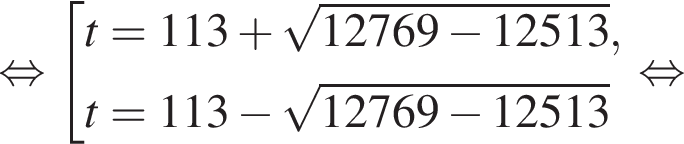
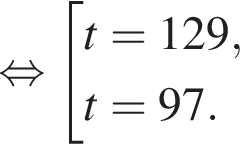
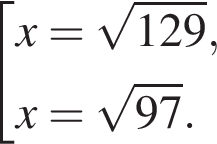
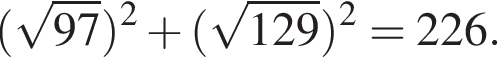
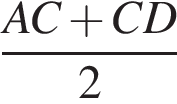 и
и 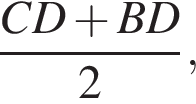 где AC, CD и BD — меньшие из возможных дуг. Тогда в треугольнике BAM по теореме о сумме углов
где AC, CD и BD — меньшие из возможных дуг. Тогда в треугольнике BAM по теореме о сумме углов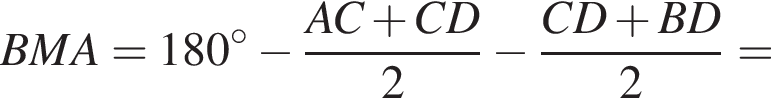
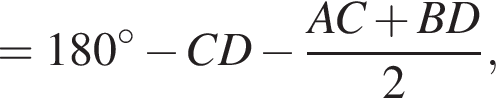

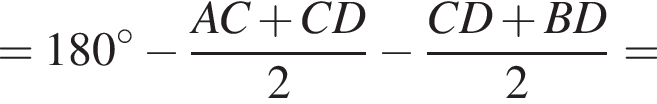
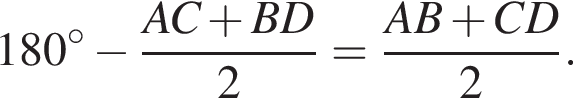 Тем самым, угол BMA равен
Тем самым, угол BMA равен 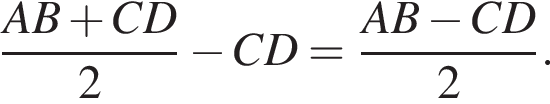
 CK = BD (по свойству параллелограмма), но BD = AС (по свойству равнобедренной трапеции), значит, CK = AC, тогда треугольник ACK — прямоугольный и равнобедренный. Найдём катеты по теореме Пифагора:
CK = BD (по свойству параллелограмма), но BD = AС (по свойству равнобедренной трапеции), значит, CK = AC, тогда треугольник ACK — прямоугольный и равнобедренный. Найдём катеты по теореме Пифагора: